my approach to maximum clique

I’ve been doing Advent of Code since high school, and this year will be my fifth year solving the problems. However, I’ve never been able to obtain all 50 stars for a problemset, because I was either too busy or gave up too soon. This year, with no pressure from school work I am determined to get those 50 stars.

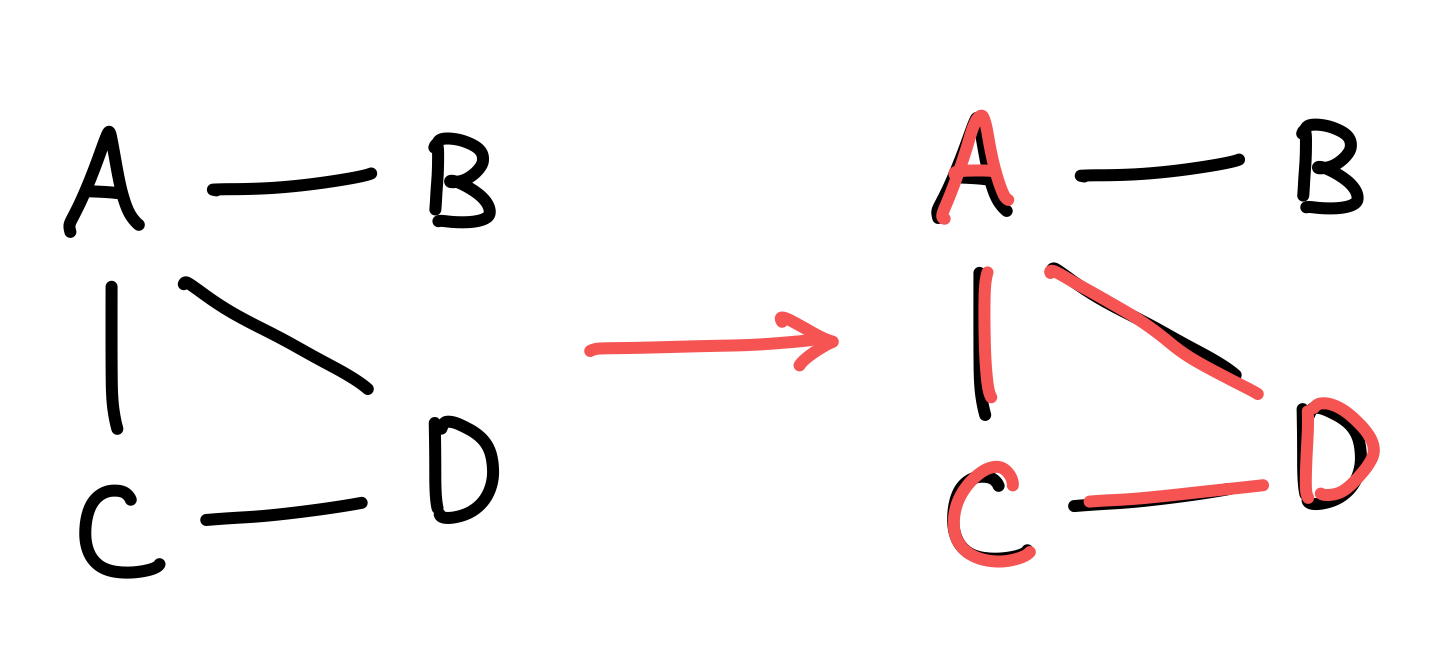
A particularly interesting problem was that of today’s, 2024 day 23 part 2. In short, it asks to solve the maximum clique problem on a relatively sparse graph, where $|E| \approx \frac{1}{6} \cdot \frac{n(n-1)}{2}$. That is, given a graph, we wish to find the connected subgraph with the most edges. The below image shows an example of this, by highlighting the found subgraph in red.

We first define the graph using an adjacency list adj. We may then define a function lcg(V), which solves the largest connected graph (LCG) problem given the nodes $V$. In the case where there is only one node, $|V| = 1$, then the LCG is simply that node. Otherwise, for each node $v$ in $V$, we find the LCG of $V$ containing $v$, denoted $LCG_v$. Then the LCG for $V$ is simply the largest of all such $LCG_v$‘s.

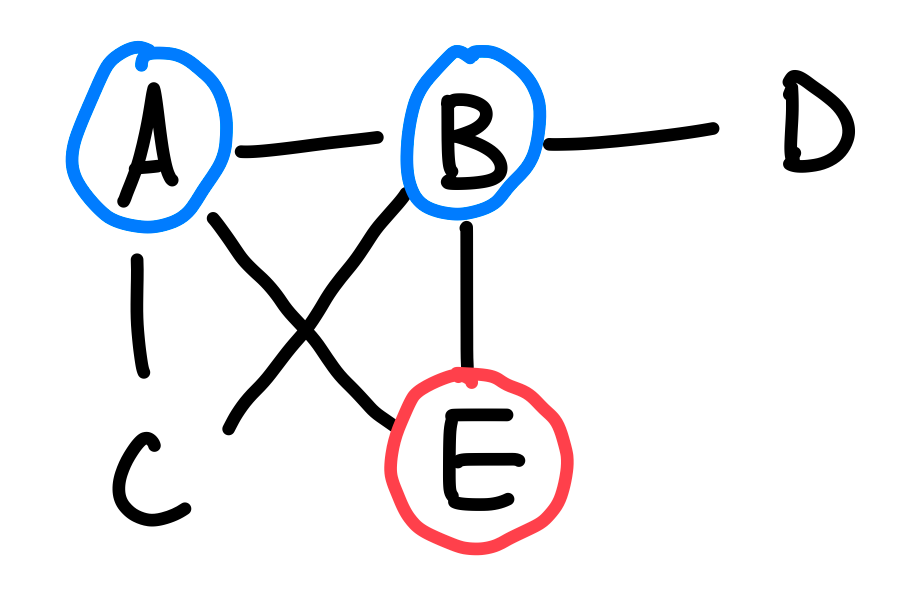
Given a node $v$, notice that $LCG_v$ can only contain its adjacent nodes that are also in $V$. So in Python notation, this is simply a call to lcg(adj[v] & V). This is illustrated by the image below. Suppose $v = E$, then for us to construct a connected graph using $E$, the only possible nodes we can use are $A$ and $B$. Nodes $C$ and $D$ are not adjacent to $E$, and therefore would not be part of a connected subgraph containing $E$. So this problem reduces to lcg({A, B, E}).

With this, I have a working version of the problem, and I verify its correctness (rather crudely) by testing it on the sample input.

def lcg(V: set[str]) -> set[str]:
    global adj

    if len(V) == 1:
        return V

    mx_lcg = set()
    for v in V:
        lcg_v = lcg(adj[v] & V) | {v}
        if len(lcg_v) > len(mx_lcg):
            mx_lcg = lcg_v
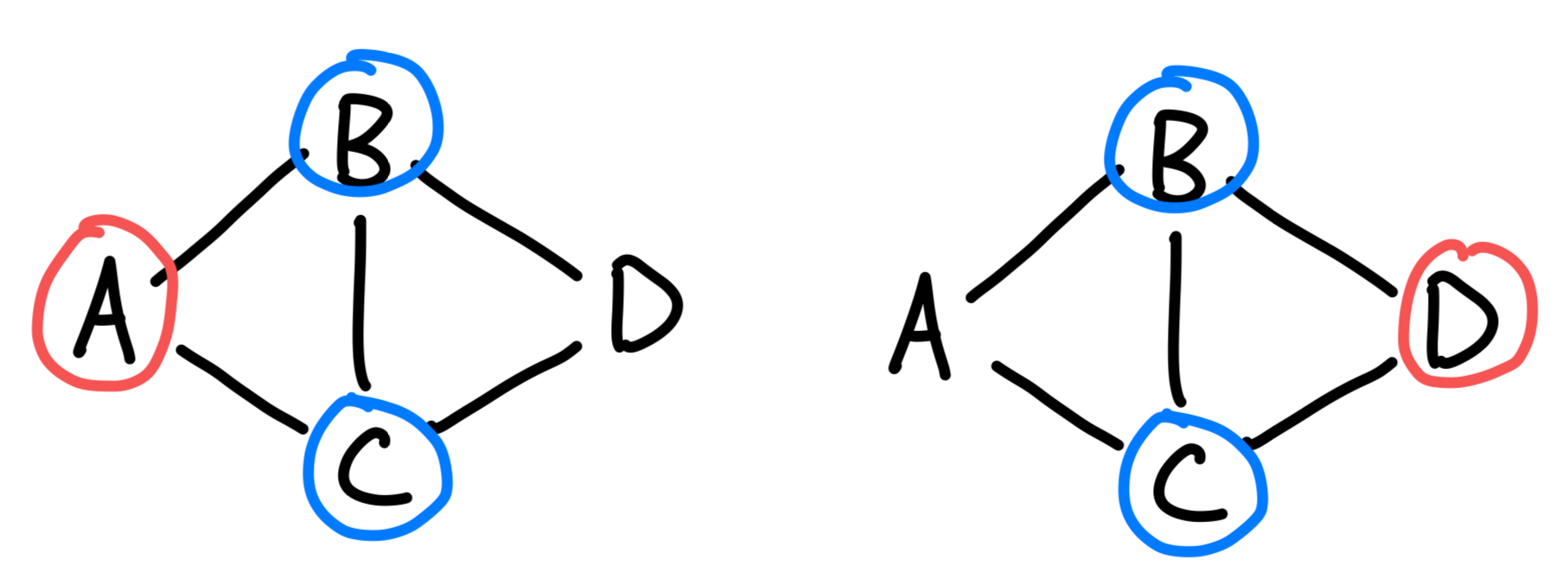
    return mx_lcg

The issue now is in performance. I realized that my code was running ridiculously slow, as it was making duplicate calls to the same set of nodes. As an example, consider the graph in the image below, with $V = \{A, B, C, D\}$. When we have $v = A$, we wish to find the LCG on $\{B, C\}$ through a call to lcg({B, C}). Now when $v = D$, we once again wish to find the LCG of $\{B, C\}$. But we already know what the answer to lcg({B, C}) is, so we don’t have to go down that computation again.

The solution to this is a classical case of dynamic programming, so I simply had to slap on a memoization lookup table. A slight problem is that Python sets aren’t hashable for use in a dictionary, so we have to convert V to a tuple first.

dp = dict()
def lcg(V: set[str]) -> set[str]:
    global adj

    if len(V) == 1:
        return V

    key = tuple(sorted(V))
    if key in dp:
        return dp[key]

    mx_lcg = set()
    for v in V:
        lcg_v = lcg(adj[v] & V) | {v}
        if len(lcg_v) > len(mx_lcg):
            mx_lcg = lcg_v

    dp[key] = mx_lcg
    return mx_lcg

And that is basically my final solution. The nice thing about this approach is that it theoretically works on any graph, and doesn’t require any hardcoding for this Advent of Code specifically.